Teoria

Curve e spline di Bézier

Nella prima fase di editing, per delineare il contorno dell'immagine da ritagliare, vengono sfruttate le curve spline di Bézier (B-spline) planari, di grado 3 e con incollamento di classe C0\mathscr{C}^0 (equivalente a G0\mathscr{G}^0). Come sono definite e cosa vuol dire classe di incollamento?

Curve di Bézier in E2\E^2

Una curva di Bézier è un particolare tipo di curva parametrica, cioè una funzione vettoriale continua del tipo: P=P(t):[0,1]→E2\P = \P(t): [0, 1] \to \E^2 con P(t)=[x(t)y(t)]\P(t) = \begin{bmatrix} x(t) \\ y(t) \end{bmatrix} e x(t),y(t)x(t), y(t) polinomi di grado k≥1k \geq 1; essa è determinata da un poligono di controllo, cioè da un insieme ordinato di k+1k + 1 punti distinti di E2\E^2 (chiamati punti di controllo).
In particolare, Bétsie sfrutta le curve cubiche di Bézier (di grado 3, k=3k = 3), definite, quindi, da un poligono di controllo costituito da k+1=4k + 1 = 4 punti in E2\E^2 solitamente indicati con {P0,P1,P2,P3}\{\P_0, \P_1, \P_2, \P_3\}. Le coordinate dei punti di controllo sono sufficienti a determinare l'equazione della curva di Bézier associata tramite l'algoritmo di de Casteljau, da cui si ottiene un'equazione del tipo:

P(t)=(1−t)3⋅P0+3(1−t)2t⋅P1+3(1−t)t2⋅P2+t3⋅P3\P(t) = (1 - t)^3\cdot\P_0 + 3(1 - t)^2t\cdot\P_1 + 3(1-t)t^2\cdot\P_2 + t^3\cdot\P_3

che, introducendo i polinomi di Bernstein di grado kk in forma generale:
Bik(t)=(ki)(1−t)k−i⋅tiB^k_i(t) = \begin{pmatrix} k \\ i \end{pmatrix}(1 - t)^{k - i} \cdot t^i con i=0,…,ki = 0, \dots, k si può riscrivere come:

P(t)=∑i=03Bi3(t)⋅Pi\displaystyle\P(t) = \sum_{i = 0}^{3}B^3_i(t)\cdot \P_i .

Quello che si vede disegnato a schermo, qui sotto in rosso, e quando utilizziamo l'applicazione, non è altro che l'immagine (o supporto) della curva così definita.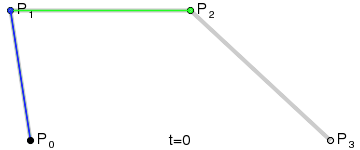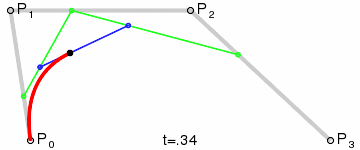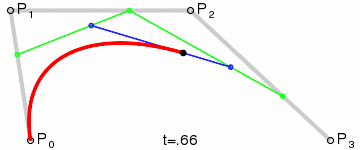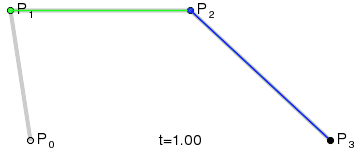

Costruzione grafica di una curva cubica di Bézier

Spline di Bézier di grado 3 in E2\E^2

Per delimitare una figura arbitrariamente complessa sarebbe necessario introdurre una curva di Bézier di grado molto elevato, che risulterebbe pesante dal punto di vista computazionale e che dipenderebbe strettamente dal suo poligono di controllo senza, quindi, offrire un controllo locale. Per risolvere questi problemi, in computer grafica si utilizzano le spline di Bézier (B-spline), cioè curve date dall'incollamento di più curve di Bézier aventi lo stesso grado: nel nostro caso, essendo tutte le curve da incollare di grado 3, si parlerà di spline cubiche (di grado k=3k = 3).
Formalmente, tutte le curve di Bézier hanno come dominio l'intervallo [0,1][0, 1] ma, per poter definire una spline, è necessario che le curve siano definite su intervalli adiacenti: questo viene fatto grazie alla possibilità di riparametrizzare una curva di Bézier definita sull'intervallo [0,1][0, 1] con una curva equivalente definita su un intervallo [a,b][a, b] arbitrario (con a<ba < b e a,b∈Ra, b \in \R). Se consideriamo t∈[0,1]t \in [0, 1] e τ∈[a,b]\tau \in [a, b] è possibile definire una funzione di transizione (biunivoca, bicontinua e bidifferenziabile):

t=t(τ)=τ−ab−at = t(\tau) = \displaystyle\frac{\tau - a}{b - a}

per due estremi aa e bb fissati che riparametrizzi una curva P(t)\P(t) in una equivalente Q(τ)\mathbf{Q}(\tau), quindi tale che: Q(τ)=P[t(τ)]\mathbf{Q}(\tau) = \P[t(\tau)].
Per far sì che i supporti di due curve cubiche P\P e Q\mathbf{Q} definite su due intervalli adiacenti [a,b][a, b] e [b,c][b, c] si incollino modo opportuno, è necessario, inoltre, definire una condizione di incollamento. Nel nostro caso utilizziamo, per dare massima libertà all'utente, la condizione di incollamento più "semplice" (chiamata C0\mathscr{C}^0 o G0\mathscr{G}^0 in caso la si consideri come condizione di incollamento geometrico) che impone solamente: P(b)=Q(b)\P(b) = \mathbf{Q}(b) e, cioè, che l'ultimo punto del poligono di controllo della prima curva coincida con il primo punto del poligono di controllo della seconda curva.

Trasformazioni affini del piano

Passando alla seconda fase di editing, invece, si possono applicare, alla porzione di immagine ritagliata, tre tipi di trasformazioni affini del piano E2\E^2, che, in pratica, sono definite sulla porzione di piano dell'intera pagina web. Teniamo in considerazione, però, che il sistema di riferimento cartesiano della pagina, con origine nell'angolo in alto a sinistra, asse delle ascisse con verso positivo a destra e asse delle ordinate con verso positivo in basso, non coincide con quello dell'immagine in primo piano che ha origine OO nel centro della stessa, asse xx positivo verso destra e asse yy positivo verso l'alto.
Le trasformazioni affini utilizzate in Bétsie, altrimenti dette affinità, sono trasformazioni di uno spazio in se stesso (E2→E2\E^2 \to \E^2); queste sono corrispondenze biunivoche che legano punti di coordinate x=(x,y)∈E2\x = (x, y) \in \E^2 a punti di coordinate x′=(x′,y′)∈E2\x' = (x', y') \in \E^2 tramite una relazione in forma matriciale del tipo:

x↦Ax+c\x \mapsto A\x + \c

dove AA è la matrice di trasformazione 2×22 \times 2 invertibile (det⁡(A)≠0\det(A) \neq 0) e c\c è un vettore fissato.
La seguente tabella mostra le caratteristiche delle tre affinità utilizzate in Bétsie:

AffinitàMatrice di trasformazione AAVettore c\c
TraslazioneI2=[1001]I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}[uv]≠[00]\begin{bmatrix} u \\ v \end{bmatrix} \neq \begin{bmatrix} 0 \\ 0 \end{bmatrix}
Rotazione di centro OO[cos⁡(θ)−sin⁡(θ)sin⁡(θ)cos⁡(θ)]\begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix}[00]\begin{bmatrix} 0 \\ 0 \end{bmatrix}
Omotetia di centro OOkI2=[k00k]kI_2 = \begin{bmatrix} k & 0 \\ 0 & k \end{bmatrix}[00]\begin{bmatrix} 0 \\ 0 \end{bmatrix}

con [uv]\begin{bmatrix} u \\ v \end{bmatrix} vettore di traslazione, θ\theta angolo di rotazione e kk fattore di dilatazione/contrazione. Ricordiamo, inoltre, che, nel nostro caso, tutte le trasformazioni hanno l'origine nel centro OO dell'immagine ritagliata di partenza.